Конические проекции
Конические проекции получаются в результате переноса поверхности Земли на боковую поверхность конуса, касательного к одной из параллелей или секущего земной шар по двум заданным параллелям. Затем конус разрезается по образующей и разворачивается на плоскость. Конические проекции в зависимости от расположения оси конуса относительно оси вращения Земли могут быть нормальные, поперечные и косые. Большинство авиационных карт построено в нормальной конической проекции.
Равноугольные конические проекции. Равноугольные конические проекции могут строиться на касательном или на секущем конусе.
Равноугольные конические проекции. Равноугольные конические проекции могут строиться на касательном или на секущем конусе.
Принцип построения такой проекции на касательном конусе (рис. 2.5) состоит в том, что все меридианы выпрямляют до соприкосновения с боковой поверхностью конуса. При этом все параллели, кроме параллели касания, будут растягиваться до размеров окружности конуса. Для того чтобы сделать проекцию равноугольной и сохранить подобие фигур, производят растягивание меридианов в такой степени, в какой были растянуты параллели в данной точке карты. Затем конус разрезается по образующей и разворачивается на плоскость.
Карты в равноугольной конической проекции на касательном конусе имеют следующие свойства:
1) меридианы изображаются в виде прямых, сходящихся к полюсу;
2) угол схождения меридианов
σ= Δλ sinφ,
где Δλ — разность долгот между заданными меридианами; φ — широта параллели касания;
3) параллели имеют вид дуг концентрических окружностей, расстояния между которыми увеличиваются по мере удаления от параллели касания;
4) на параллели касания искажения длин отсутствуют, а в полосе ±5° от этой параллели они незначительные и в практике не учитываются;
5) локсодромия изображается кривой линией, обращенной своей выпуклостью к экватору;
6) ортодромия для расстояний до 1200 км изображается прямой линией, а для больших расстояний имеет вид кривой, обращенной своей выпуклостью в сторону более крупного масштаба.
В равноугольной конической проекции на касательном конусе издаются бортовые карты масштабов 1:2000000, 1:2500000, 1 :3 000 000, 1 : 4 000 000 и обзорная карта масштаба 1 :5 000 000.
Карты в равноугольной конической проекции на касательном конусе имеют следующие свойства:
1) меридианы изображаются в виде прямых, сходящихся к полюсу;
2) угол схождения меридианов
σ= Δλ sinφ,
где Δλ — разность долгот между заданными меридианами; φ — широта параллели касания;
3) параллели имеют вид дуг концентрических окружностей, расстояния между которыми увеличиваются по мере удаления от параллели касания;
4) на параллели касания искажения длин отсутствуют, а в полосе ±5° от этой параллели они незначительные и в практике не учитываются;
5) локсодромия изображается кривой линией, обращенной своей выпуклостью к экватору;
6) ортодромия для расстояний до 1200 км изображается прямой линией, а для больших расстояний имеет вид кривой, обращенной своей выпуклостью в сторону более крупного масштаба.
В равноугольной конической проекции на касательном конусе издаются бортовые карты масштабов 1:2000000, 1:2500000, 1 :3 000 000, 1 : 4 000 000 и обзорная карта масштаба 1 :5 000 000.
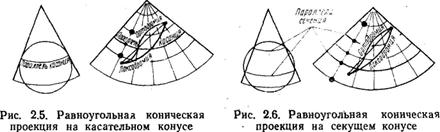
С целью уменьшения искажений поверхность Земли переносят на секущий конус (рис. 2.6). Равноугольная коническая проекция на секущем конусе имеет следующие свойства:
1) угол схождения меридианов определяется по формуле
σ= Δλ sinφср,
где Δλ — разность долгот между заданными меридианами; φср — средняя широта между параллелями сечения;
2) на параллелях сечения искажения длин отсутствуют, а в полосе ±5° от этих параллелей искажения незначительные;
3) масштаб в разных точках карты неодинаковый. На внешних сторонах от параллелей сечения он крупнее, а между параллелями сечения мельче. Такое изменение масштабов обусловлено тем, что при переносе поверхности Земли на секущий конус изображения на внешних сторонах от параллелей сечения, приходится растягивать, а между параллелями сечения сжимать;
4) ортодромия изображается кривой, выпуклой в сторону более крупного масштаба и имеет точку перегиба на параллели наименьшего масштаба.
В нормальной равноугольной конической про- екции на секущем конусе издаются бортовые карты масштабов 1 :2 000 000 (Москва — Берлин) и 1 : 2 500 000.
1) угол схождения меридианов определяется по формуле
σ= Δλ sinφср,
где Δλ — разность долгот между заданными меридианами; φср — средняя широта между параллелями сечения;
2) на параллелях сечения искажения длин отсутствуют, а в полосе ±5° от этих параллелей искажения незначительные;
3) масштаб в разных точках карты неодинаковый. На внешних сторонах от параллелей сечения он крупнее, а между параллелями сечения мельче. Такое изменение масштабов обусловлено тем, что при переносе поверхности Земли на секущий конус изображения на внешних сторонах от параллелей сечения, приходится растягивать, а между параллелями сечения сжимать;
4) ортодромия изображается кривой, выпуклой в сторону более крупного масштаба и имеет точку перегиба на параллели наименьшего масштаба.
В нормальной равноугольной конической про- екции на секущем конусе издаются бортовые карты масштабов 1 :2 000 000 (Москва — Берлин) и 1 : 2 500 000.