Навигационный треугольник скоростей, его элементы и их взаимозависимость
Самолет относительно воздушной массы перемещается с воздушной скоростью в направлении своей продольной оси. Одновременно под действием ветра он перемещается вместе с воздушной массой в направлении и со скоростью ее движения. В результате движение самолета относительно земной поверхности будет происходить по равнодействующей, построенной на слагаемых скоростях самолета и ветра. Таким образом, при полете с боковым ветром векторы воздушной скорости, путевой скорости и скорости ветра образуют треугольник (рис. 7.3), который называется навигационным треугольником скоростей. Каждый вектор характеризуется направлением и величиной.
Вектором воздушной скорости называется направление и скорость движения самолета относительно воздушных масс. Его направление определяется курсом самолета, а величина — значением воздушной скорости.
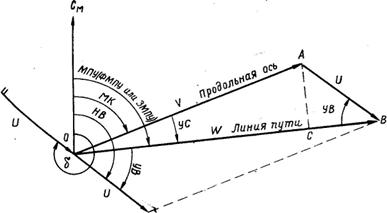
Рис. 7.3. Навигационный треугольник скоростей и его элементы
Вектором путевой скорости называется направление и скорость движения самолета относительно земной поверхности. Его направление определяется путевым углом, а величина — значением путевой скорости.
Вектором ветра называется направление и скорость движения воздушной массы относительно земной поверхности. Его направление определяется направлением ветра, а величина — значением его скорости.
Навигационный треугольник скоростей имеет следующие элементы:
МК — магнитный курс самолета;
V — воздушная скорость;
МПУ— магнитный путевой угол (может быть заданным —ЗМПУ и фактическим — ФМПУ);
W — путевая скорость;
НВ — навигационное направление ветра;
U — скорость ветра;
УС — угол сноса;
УВ — угол ветра.
Фактическим магнитным путевым углом называется угол, заключенный между северным направлением магнитного меридиана и линией фактического пути. Отсчитывается от северного направления магнитного меридиана до линии фактического пути по ходу часовой стрелки от 0 до 360°.
Углом сноса называется угол, заключенный между продольной осью самолета и линией пути. Отсчитывается от продольной оси самолета до линии пути вправо со знаком плюс и влево со знаком минус.
Углом ветра называется угол, заключенный между линией пути (фактической или заданной) и направлением навигационного ветра. Отсчитывается от линии пути до направления ветра по ходу часовой стрелки от 0 до 360°.
Между элементами навигационного треугольника скоростей существует следующая зависимость:
МК = МПУ - (± УС);
ОС = V cos УС;
МПУ = МК + (± УС);
CB = U cos УВ;
УС = МПУ-МК; W = VсоsУС + UсоsУВ;
УВ = δ ± 180° - МПУ; δ = МПУ + УВ ± 180°.
Так как углы сноса обычно небольшие, а косинусы малых углов близки к единице, то можно считать, что W ≈ V+UсоsУВ. Приведенные выше формулы используются для расчета элементов навигационного треугольника скоростей.
Угол сноса и путевая скорость являются основными навигационными элементами, поэтому нужно твердо знать, как они зависят от изменения воздушной скорости, скорости ветра и угла ветра.
Зависимость угла сноса и путевой скорости от воздушной скорости самолета. При неизменном ветре и курсе самолета путевая скорость изменяется соответственно изменению воздушной скорости, т. е. с увеличением воздушной скорости путевая скорость становится больше, а с уменьшением — меньше (рис. 7.4). Считают, что изменение воздушной скорости вызывает пропорциональное изменение путевой скорости, т. е. насколько изменилась воздушная скорость, настолько соответственно изменится и путевая скорость.
Вектором воздушной скорости называется направление и скорость движения самолета относительно воздушных масс. Его направление определяется курсом самолета, а величина — значением воздушной скорости.

Рис. 7.3. Навигационный треугольник скоростей и его элементы
Вектором путевой скорости называется направление и скорость движения самолета относительно земной поверхности. Его направление определяется путевым углом, а величина — значением путевой скорости.
Вектором ветра называется направление и скорость движения воздушной массы относительно земной поверхности. Его направление определяется направлением ветра, а величина — значением его скорости.
Навигационный треугольник скоростей имеет следующие элементы:
МК — магнитный курс самолета;
V — воздушная скорость;
МПУ— магнитный путевой угол (может быть заданным —ЗМПУ и фактическим — ФМПУ);
W — путевая скорость;
НВ — навигационное направление ветра;
U — скорость ветра;
УС — угол сноса;
УВ — угол ветра.
Фактическим магнитным путевым углом называется угол, заключенный между северным направлением магнитного меридиана и линией фактического пути. Отсчитывается от северного направления магнитного меридиана до линии фактического пути по ходу часовой стрелки от 0 до 360°.
Углом сноса называется угол, заключенный между продольной осью самолета и линией пути. Отсчитывается от продольной оси самолета до линии пути вправо со знаком плюс и влево со знаком минус.
Углом ветра называется угол, заключенный между линией пути (фактической или заданной) и направлением навигационного ветра. Отсчитывается от линии пути до направления ветра по ходу часовой стрелки от 0 до 360°.
Между элементами навигационного треугольника скоростей существует следующая зависимость:
МК = МПУ - (± УС);
ОС = V cos УС;
МПУ = МК + (± УС);
CB = U cos УВ;
УС = МПУ-МК; W = VсоsУС + UсоsУВ;
УВ = δ ± 180° - МПУ; δ = МПУ + УВ ± 180°.
Так как углы сноса обычно небольшие, а косинусы малых углов близки к единице, то можно считать, что W ≈ V+UсоsУВ. Приведенные выше формулы используются для расчета элементов навигационного треугольника скоростей.
Угол сноса и путевая скорость являются основными навигационными элементами, поэтому нужно твердо знать, как они зависят от изменения воздушной скорости, скорости ветра и угла ветра.
Зависимость угла сноса и путевой скорости от воздушной скорости самолета. При неизменном ветре и курсе самолета путевая скорость изменяется соответственно изменению воздушной скорости, т. е. с увеличением воздушной скорости путевая скорость становится больше, а с уменьшением — меньше (рис. 7.4). Считают, что изменение воздушной скорости вызывает пропорциональное изменение путевой скорости, т. е. насколько изменилась воздушная скорость, настолько соответственно изменится и путевая скорость.
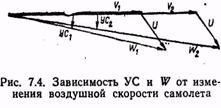
Угол сноса с возрастанием воздушной скорости уменьшается, а с ее уменьшением — увеличивается.
Зависимость утла сноса и путевой скорости от скорости ветра.
При постоянной воздушной скорости и курсе самолета с увеличением скорости ветра угол сноса увеличивается, а при ее уменьшении — уменьшается (рис. 7.5).
Путевая скорость при попутном и попутно-боковом ветре с изменением скорости ветра изменяется так же, как и угол сноса. При встречном и встречно-боковом ветре с увеличением скорости ветра путевая скорость уменьшается, а с уменьшением —увеличивается.
Зависимость утла сноса и путевой скорости от скорости ветра.
При постоянной воздушной скорости и курсе самолета с увеличением скорости ветра угол сноса увеличивается, а при ее уменьшении — уменьшается (рис. 7.5).
Путевая скорость при попутном и попутно-боковом ветре с изменением скорости ветра изменяется так же, как и угол сноса. При встречном и встречно-боковом ветре с увеличением скорости ветра путевая скорость уменьшается, а с уменьшением —увеличивается.

Рис. 7.5. Зависимость УС и W от изменения скорости ветра: а —при попутно-боковом ветре; б —при встречно-боковом ветре
Зависимость угла сноса и путевой скорости от угла ветра. Угол ветра в полете не остается постоянным. Его величина изменяется в полете как вследствие изменения направления ветра, так и вследствие изменения направления полета.
Отложим в определенном масштабе вектор воздушной скорости (рис. 7.6).
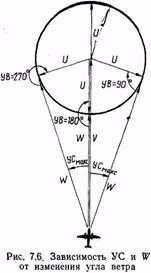
Из конца этого вектора радиусом, равным скорости ветра в том же масштабе, опишем окружность. Если перемещать вектор ветра по ходу часовой стрелки, то угол ветра будет изменяться.
Угол сноса и путевая скорость зависят от угла ветра следующим образом:
1. При УВ = 0° (ветер попутный)
УС=0,W=V+U
2. При увеличении угла ветра от 0 до 90° угол сноса увеличивается, а путевая скорость уменьшается.
3. При УВ = 90° (ветер боковой) угол сноса максимальный, а путевая скорость примерно равна воздушной .
4. При увеличении УВ от 90 до 180° угол сноса и путевая скорость уменьшаются.
5. При УВ = 180° (ветер встречный) УС==0°, a W=V— U.
6. При увеличении УВ от 180 до 270° угол сноса и путевая скорость увеличиваются.
7. При УВ = 270° (ветер боковой) угол сноса максимальный, а путевая скорость примерно равна воздушной.
8. При увеличении УВ от 270 до 360° угол сноса уменьшается, а путевая скорость увеличивается.
При решении большинства навигационных задач необходимо ясно представлять, в какую сторону при данном угле ветра будет направлен снос самолета и какова его путевая скорость (больше или меньше воздушной).
Угол сноса и путевая скорость зависят от угла ветра следующим образом:
1. При УВ = 0° (ветер попутный)
УС=0,W=V+U
2. При увеличении угла ветра от 0 до 90° угол сноса увеличивается, а путевая скорость уменьшается.
3. При УВ = 90° (ветер боковой) угол сноса максимальный, а путевая скорость примерно равна воздушной .
4. При увеличении УВ от 90 до 180° угол сноса и путевая скорость уменьшаются.
5. При УВ = 180° (ветер встречный) УС==0°, a W=V— U.
6. При увеличении УВ от 180 до 270° угол сноса и путевая скорость увеличиваются.
7. При УВ = 270° (ветер боковой) угол сноса максимальный, а путевая скорость примерно равна воздушной.
8. При увеличении УВ от 270 до 360° угол сноса уменьшается, а путевая скорость увеличивается.
При решении большинства навигационных задач необходимо ясно представлять, в какую сторону при данном угле ветра будет направлен снос самолета и какова его путевая скорость (больше или меньше воздушной).
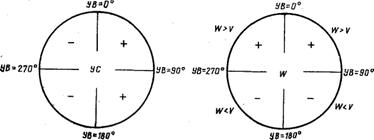
Рис. 7.7. Правила определения W и знаков УС
Изменение угла ветра приводит к следующему изменению угла сноса и путевой скорости (рис. 7.7): при углах ветра 0—180° углы сноса положительные, а при углах ветра 180—360° — отрицательные; путевая скорость при углах ветра 270—0—90° больше воздушной скорости, а при углах ветра 90—180—270° меньше.
Пример. ЗМПУ=100°; δ=40°. Определить, в какую сторону направлен снос самолета и какова его путевая скорость.
Решение. 1. Находим угол ветра:
УВ = δ ± 180° — ЗМПУ = 40° + 180° — 100° = 120°.
2. Определяем знак угла сноса и путевую скорость. Так как УВ в пределах от 0 до 180°, то угол сноса будет положительный, а путевая скорость меньше воздушной.
Максимальным называется угол сноса при углах ветра 90 и 270° (см. рис. 7.6). Его величина определятся по формуле
sinУСмакс=U/V
При современных скоростях полета величина угла сноса обычно не превышает 10—20°. Известно, что синусы малых углов можно принять равными самим углам, выраженным в радианах. 1 рад—57°,3 или округленно 60°.
На основании этого можно записать, что
sinУСмакс=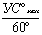
Следовательно,
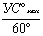 =U/V, откуда УСмакс =
=U/V, откуда УСмакс = 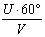
Из формулы видно, что УС тем больше, чем меньше воздушная скорость полета и чем больше скорость ветра.
Пример. V=360 км/ч; U=60 км/ч. Определить максимальный угол сноса.
Решение. УСмакс =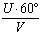 =
=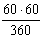 =10°
=10°
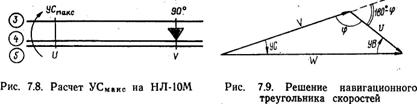
Обычно максимальный угол сноса рассчитывается с помощью НЛ-10М (рис. 7.8).
Пример. ЗМПУ=100°; δ=40°. Определить, в какую сторону направлен снос самолета и какова его путевая скорость.
Решение. 1. Находим угол ветра:
УВ = δ ± 180° — ЗМПУ = 40° + 180° — 100° = 120°.
2. Определяем знак угла сноса и путевую скорость. Так как УВ в пределах от 0 до 180°, то угол сноса будет положительный, а путевая скорость меньше воздушной.
Максимальным называется угол сноса при углах ветра 90 и 270° (см. рис. 7.6). Его величина определятся по формуле
sinУСмакс=U/V
При современных скоростях полета величина угла сноса обычно не превышает 10—20°. Известно, что синусы малых углов можно принять равными самим углам, выраженным в радианах. 1 рад—57°,3 или округленно 60°.
На основании этого можно записать, что
sinУСмакс=
Следовательно,
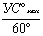 =U/V, откуда УСмакс =
=U/V, откуда УСмакс = 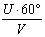
Из формулы видно, что УС тем больше, чем меньше воздушная скорость полета и чем больше скорость ветра.
Пример. V=360 км/ч; U=60 км/ч. Определить максимальный угол сноса.
Решение. УСмакс =
Обычно максимальный угол сноса рассчитывается с помощью НЛ-10М (рис. 7.8).