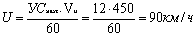Решение навигационного треугольника скоростей
Решить навигационный треугольник скоростей — это значит по его известным элементам найти неизвестные. Решение навигационного треугольника скоростей можно осуществить:
1) графически (на бумаге);
2) с помощью навигационной линейки, навигационного расчетчика или ветрочета;
3) приближенно подсчетом в уме.
1) графически (на бумаге);
2) с помощью навигационной линейки, навигационного расчетчика или ветрочета;
3) приближенно подсчетом в уме.
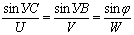
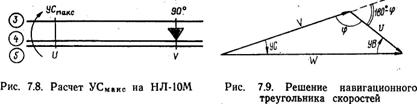
Так как sinφ= sin (180°—φ), а внешний угол треугольника равен сумме внутренних углов, не смежных с ним, т. е. угол 180°—φ=УВ+УС, приведенные выше отношения записываются в таком виде:
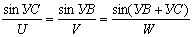
1) при углах ветра 0—180° углы сноса положительные;
2) при углах ветра 180—360° углы сноса отрицательные;
3) при углах ветра больше 180° на НЛ-10М устанавливают его дополнение до 360°, т. е. разность 360°—УВ;
4) при угле ветра, равном нулю, W=V+U, а при угле ветра, равном 180°, W=V—U; для других значений углов ветра путевая скорость отсчитывается по НЛ-10М против суммы УВ+УС, при нахождении которой к УВ прибавляется всегда абсолютная величина УС независимо от его знака;
5) для углов ветра в пределах 5—175° используется шкала синусов, а в пределах 0,5—5 и 175—179,5° — шкала тангенсов.
Отсчет угла сноса для расчета курса следования производится с точностью до 1°, а для точного определения путевой скорости при углах ветра, близких к 0 и 180°, — с точностью до десятых долей градуса;
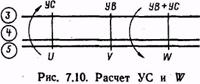
При помощи навигационной линейки определяются угол сноса и путевая скорость, а затем рассчитываются курс следования и время полета на заданном участке трассы.
Курсом следования называется курс, рассчитанный с учетом угла сноса для следования по линии заданного пути. Для каждого участка трассы полета курс следования, угол сносами путевая скорость перед полетом определяются по прогностическому, а в полете по измеренному ветру.
Пример. Vи=460 км/ч; ЗМПУ=105°; δ = 330°; U=80 км/ч; S = 120 км. Определить УС, W, МКсл и t.
Решение. 1. Находим угол ветра:
УВ = δ ± 180° — ЗМПУ = 330°—180° — 105° = 45°.
2. Определяем угол сноса и путевую скорость (см. ключ для НЛ-10М на рис. 7.10): УСЗ=+7°; W=512 км/ч.
3. Рассчитываем магнитный курс следования:
МКсл = ЗМПУ — (± УС) = 105° — (+ 7°) = 98°.
4. Определяем с помощью НЛ-10М время полета: t=14 мин.
Если известны угол сноса, путевая и воздушная скорости, магнитный курс самолета, то с помощью НЛ-10М можно определить ветер. Для решения этой задачи рассмотрим навигационный треугольник скоростей (рис. 7.11).
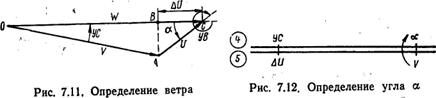
Из конца вектора воздушной скорости опустим на линию пути перпендикуляр. Величина путевой скорости может быть представлена в виде суммы двух отрезков: ОВ и ВС, т. е. W=OB+ВС, откуда отрезок ВС= W—ОВ.
Из прямоугольного треугольника ОАВ следует, что отрезок ОВ = VсоsУС. Так как косинусы малых углов примерно равны 1, то отрезок ОВ можно принять равным V(OB ≈ V). Подставляя это значение ОВ в выражение для отрезка ВС, получаем: ВС= W—V=ΔU.
Из прямоугольных треугольников АВО и ABC имеем:
АВ = VtgУС=ΔUtg или VtgУC= ΔUtgα.
Запишем это равенство в виде следующей пропорции, имея в виду ее основное свойство:
tgУC/ΔU= tgα/V.
Решая эту пропорцию на НЛ-10М по шкалам 4 и 5, можно определить угол а (рис. 7.12), заключенный между линией фактического пути и метеорологическим направлением ветра. Измеряется этот угол от 0 до 90°. Зная величину угла а и используя шкалы 3 и 5 НЛ-10М, по теореме синусов определим скорость ветра (рис. 7.13).
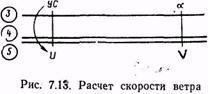
Направление ветра рассчитывается по формулам:
δ = ФМПУ-(±α)
δ = ФМПУ ± 180°+ (± α).
Первой формулой пользуются, когда путевая скорость меньше воздушной, т. е. при встречно-боковом ветре, а второй — при попутно-боковом ветре, когда путевая скорость больше воздушной. Угол α берется со знаком плюс при правом сносе самолета и со знаком минус при левом сносе.
Для быстрого и правильного определения метеорологического направления ветра и его скорости необходимо запомнить следующие правила:
1. При попутном ветре (УС=0, α = 0°):
δ = ФМПУ ± 180°; U = W — Vи.
2. При встречном ветре (УС=0°, α=0°):
δ = ФМПУ; U = Vи — W.
3. При боковом ветре (W ≈ Vи, α=90°):
δ= ФМПУ —(±90°).
4. При встречно-боковом ветре (W< Vи):
δ = ФМПУ — (± α).
5. При попутно-боковом ветре (W> Vи):
δ = ФМПУ ± 180°+ (± α).
Пример. Vи = 450 км/ч; МК = 50°; УС = + 7°; W = 490 км/ч. Определить направление и скорость ветра.
Решение. 1. Находим разность между путевой и истинной воздушной скоростью; ΔU = W — Vи =490 — 450 = + 40 км/ч. Ветер попутно-боковой
2. Определяем угол α на НЛ-10М (см. рис. 7.12): α =+ 54°.
3. Находим скорость ветра на НЛ-10М (см. рис. 7.13): U = 68 км/ч.
4. Опрепеляем ФМПУ и метеорологическое направление ветра
ФМПУ = МК + (± УС) = 50° + (+ 7°) = 57°;
δ = ФМПУ ± 180° + (±α) = 57° + 180° + (+ 54°) = 291°.
Понятие об эквивалентном ветре. Для упрощения выполнения некоторых навигационных расчетов пользуются эквивалентным ветром.
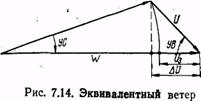 Эквивалентным ветром Uэ называется условный ветер, направление которого всегда совпадает с ЛЗП, а его скорость в сумме с воздушной скоростью дает такую же путевую скорость, как и действительный ветер (рис. 7.14).
Эквивалентным ветром Uэ называется условный ветер, направление которого всегда совпадает с ЛЗП, а его скорость в сумме с воздушной скоростью дает такую же путевую скорость, как и действительный ветер (рис. 7.14).
Эквивалентный ветер определяется по специальной таблице,
которая помещается в руководстве по летной эксплуатации и пилотированию каждого типа самолета. Приближенно эквивалентный ветер можно определить по формуле
Uэ ≈ UсоsУВ.
Решение навигационного треугольника скоростей подсчетом в уме.
Подсчетом в уме определяют угол сноса, путевую скорость и курс следования, а также направление и скорость ветра по известным значениям воздушной и путевой скоростей, магнитному курсу и углу сноса.
Угол сноса и путевую скорость можно определить, пользуясь формулами:
УС=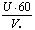 sinУВ; W = Vи ±UсоsУВ,по которым рассчитывается таблица значений углов сноса и путевых скоростей для основных углов ветра (табл. 7.1). Эту таблицу необходимо знать на память.
sinУВ; W = Vи ±UсоsУВ,по которым рассчитывается таблица значений углов сноса и путевых скоростей для основных углов ветра (табл. 7.1). Эту таблицу необходимо знать на память.
Таблица 7. 1
Зависимость угла сноса и путевой скорости от угла ветра
Пример. Vи = 450 км/ч; ЗМПУ=;120°; δ = 30°; U=60 км/ч. Определить УС, МКсл и W.
Решение. 1. Находим угол ветра:
УВ = δ ± 180° — ЗМПУ = 30° + 180° — 120° = 90°.
2. Определяем угол сноса. Так как угол ветра равен 90°, то УС = УСмакс.
УСмакс =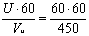 =+8°
=+8°
3. Определяем путевую скорость самолета. Поскольку ветер боковой W ≈ Vи =450км/ч.
4. Определяем курс следования:
МКсл = ЗМПУ — (± УС) = 120° —(+ 8°) = 112°.
Направление и скорость ветра в некоторых случаях можно определять подсчетом в уме.
При попутном ветре, когда УС = 0°, а путевая скорость больше воздушной скорости, направление и скорость ветра определяются по приведенным выше формулам:
δ = ФМПУ ± 180°; U = W —Vи
При встречном ветре, когда УС = 0°, а путевая скорость меньше воздушной скорости, направление и скорость ветра определяются по формулам:
δ = ФМПУ; U = Vи —W.
При боковом ветре, когда угол сноса положительный (α = +90°) или отрицательный (α = —90°), а путевая скорость равна воздушной скорости, направление и скорость ветра определяются по формулам:
δ = ФМПУ-(±90°); U =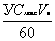 .
.
Пример. МК=202°; УС= —12°; Vи = 450 км/ч; W = 450 км/ч. Определить направление и скорость ветра.
Решение. 1. ФМПУ=МК+(±УС) = 202°+(—12°) = 190°.
2. δ = ФМПУ — (± α) = 190° — (—90°) = 280°
3.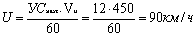
Из прямоугольного треугольника ОАВ следует, что отрезок ОВ = VсоsУС. Так как косинусы малых углов примерно равны 1, то отрезок ОВ можно принять равным V(OB ≈ V). Подставляя это значение ОВ в выражение для отрезка ВС, получаем: ВС= W—V=ΔU.
Из прямоугольных треугольников АВО и ABC имеем:
АВ = VtgУС=ΔUtg или VtgУC= ΔUtgα.
Запишем это равенство в виде следующей пропорции, имея в виду ее основное свойство:
tgУC/ΔU= tgα/V.
Решая эту пропорцию на НЛ-10М по шкалам 4 и 5, можно определить угол а (рис. 7.12), заключенный между линией фактического пути и метеорологическим направлением ветра. Измеряется этот угол от 0 до 90°. Зная величину угла а и используя шкалы 3 и 5 НЛ-10М, по теореме синусов определим скорость ветра (рис. 7.13).

Направление ветра рассчитывается по формулам:
δ = ФМПУ-(±α)
δ = ФМПУ ± 180°+ (± α).
Первой формулой пользуются, когда путевая скорость меньше воздушной, т. е. при встречно-боковом ветре, а второй — при попутно-боковом ветре, когда путевая скорость больше воздушной. Угол α берется со знаком плюс при правом сносе самолета и со знаком минус при левом сносе.
Для быстрого и правильного определения метеорологического направления ветра и его скорости необходимо запомнить следующие правила:
1. При попутном ветре (УС=0, α = 0°):
δ = ФМПУ ± 180°; U = W — Vи.
2. При встречном ветре (УС=0°, α=0°):
δ = ФМПУ; U = Vи — W.
3. При боковом ветре (W ≈ Vи, α=90°):
δ= ФМПУ —(±90°).
4. При встречно-боковом ветре (W< Vи):
δ = ФМПУ — (± α).
5. При попутно-боковом ветре (W> Vи):
δ = ФМПУ ± 180°+ (± α).
Пример. Vи = 450 км/ч; МК = 50°; УС = + 7°; W = 490 км/ч. Определить направление и скорость ветра.
Решение. 1. Находим разность между путевой и истинной воздушной скоростью; ΔU = W — Vи =490 — 450 = + 40 км/ч. Ветер попутно-боковой
2. Определяем угол α на НЛ-10М (см. рис. 7.12): α =+ 54°.
3. Находим скорость ветра на НЛ-10М (см. рис. 7.13): U = 68 км/ч.
4. Опрепеляем ФМПУ и метеорологическое направление ветра
ФМПУ = МК + (± УС) = 50° + (+ 7°) = 57°;
δ = ФМПУ ± 180° + (±α) = 57° + 180° + (+ 54°) = 291°.
Понятие об эквивалентном ветре. Для упрощения выполнения некоторых навигационных расчетов пользуются эквивалентным ветром.

Эквивалентный ветер определяется по специальной таблице,
которая помещается в руководстве по летной эксплуатации и пилотированию каждого типа самолета. Приближенно эквивалентный ветер можно определить по формуле
Uэ ≈ UсоsУВ.
Решение навигационного треугольника скоростей подсчетом в уме.
Подсчетом в уме определяют угол сноса, путевую скорость и курс следования, а также направление и скорость ветра по известным значениям воздушной и путевой скоростей, магнитному курсу и углу сноса.
Угол сноса и путевую скорость можно определить, пользуясь формулами:
УС=
Таблица 7. 1
Зависимость угла сноса и путевой скорости от угла ветра
| Угол ветра, град |
Угол сноса, град |
Путевая скорость, км/ч |
| 0 | 0 | Vи + U |
| 45 | + 0,7УСмакс | Vи + 0,7U |
| 90 | + УСмакс | Vи |
| 135 | + 0,7УСмакс |
Vи и – 0,7U |
| 180 | 0 | Vи – U |
| 225 | — 0,7УСмакс |
Vи – 0,7U |
| 270 | — УСмакс | Vи |
| 315 | — 0,7макс | Vи + 0,7U |
Пример. Vи = 450 км/ч; ЗМПУ=;120°; δ = 30°; U=60 км/ч. Определить УС, МКсл и W.
Решение. 1. Находим угол ветра:
УВ = δ ± 180° — ЗМПУ = 30° + 180° — 120° = 90°.
2. Определяем угол сноса. Так как угол ветра равен 90°, то УС = УСмакс.
УСмакс =
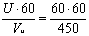 =+8°
=+8°3. Определяем путевую скорость самолета. Поскольку ветер боковой W ≈ Vи =450км/ч.
4. Определяем курс следования:
МКсл = ЗМПУ — (± УС) = 120° —(+ 8°) = 112°.
Направление и скорость ветра в некоторых случаях можно определять подсчетом в уме.
При попутном ветре, когда УС = 0°, а путевая скорость больше воздушной скорости, направление и скорость ветра определяются по приведенным выше формулам:
δ = ФМПУ ± 180°; U = W —Vи
При встречном ветре, когда УС = 0°, а путевая скорость меньше воздушной скорости, направление и скорость ветра определяются по формулам:
δ = ФМПУ; U = Vи —W.
При боковом ветре, когда угол сноса положительный (α = +90°) или отрицательный (α = —90°), а путевая скорость равна воздушной скорости, направление и скорость ветра определяются по формулам:
δ = ФМПУ-(±90°); U =
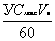 .
.Пример. МК=202°; УС= —12°; Vи = 450 км/ч; W = 450 км/ч. Определить направление и скорость ветра.
Решение. 1. ФМПУ=МК+(±УС) = 202°+(—12°) = 190°.
2. δ = ФМПУ — (± α) = 190° — (—90°) = 280°
3.